- 문제설명
토끼와 거북이는 수천년째 달리기 시합을 하고 있습니다. 어느덧 시간이 흘러 21세기가 되었고, 토끼와 거북이의 달리기를 학습한 인공지능 모델이 등장했습니다. 두 가상 동물은 2차원 메타버스 세계에서 달리기 시합을 하게 되었습니다.
달리기 시합의 승자는 미로의 맨 위 왼쪽 칸(1행 1열)에서 출발해 미로의 맨 아래 오른쪽 칸(N행 M열)에 먼저 도착하는 쪽입니다. 미로의 각 칸은 벽 또는 빈 칸으로, 토끼와 거북이 모두 벽을 넘거나 부술 수 없습니다. 미로의 테두리(1행의 위, N행의 아래, 1열의 왼쪽, M열의 오른쪽)는 모두 벽으로 막혀 있습니다.
토끼는 1분에 한 번 상하좌우 중 한 방향으로 최대 2칸 이동합니다. 토끼의 이동을 조금 더 자세하게 서술하겠습니다. 우선 이동할 방향을 정하고, 1칸 이동합니다. 같은 방향으로 1칸 더 이동할 수 있다면 반드시 이동해야 하며, 아니라면 거기서 멈춥니다. 첫 번째 예시 입력을 예로 들면, 토끼 로봇이 오른쪽 - 아래 - 오른쪽 순으로 이동할 때 그의 위치는 1행 1열 - 1행 2열 - 3행 2열 - 3행 4열 순입니다.
미로의 모습이 입력으로 주어집니다. 토끼가 미로의 맨 위 왼쪽 칸에서 출발해 미로의 맨 아래 오른쪽 칸으로 이동하는데 적어도 몇 분이 걸리는지 출력하는 프로그램을 작성하세요.
- 입출력 예
입력 #1
3 4
..##
#.##
....
입력 #2
5 4
....
#.##
..#.
....
..#.
- 입력값 설명
첫째 줄에 미로의 세로 너비 N과 가로 너비 M이 주어집니다. (2 ≤ N ≤ 50, 2 ≤ M ≤ 50)
둘째 줄부터 N개의 줄에 걸쳐 미로의 정보가 주어집니다. #는 벽을 나타내며, .는 빈 칸을 나타냅니다.
출력 #1
3
출력 #2
-1
- 출력값 설명
토끼가 미로의 맨 위 왼쪽 칸에서 출발해 미로의 맨 아래 오른쪽 칸으로 이동하는데 몇 분이 걸리는지 출력합니다.
어떻게 이동해도 맨 아래 오른쪽 칸에 도달하지 못한다면 대신 -1을 출력합니다.
- 문제 풀이
이번 스터디문제는 미로찾기 문제로, BFS(너비 우선 탐색)을 함께 공부하고자 선정해 보았습니다.
DFS(깊이 우선 탐색)도 가능하지만 특정 경로를 깊게 탐색하기 때문에 비효율적일 수 있으며 인접한 점을 통해 최단 경로를 구하는 방식은 BFS로 풀어나가는 것이 효율적이기 때문입니다.
하지만 단순한 미로찾기 문제에서 토끼가 반드시 2칸을 이동하고 그렇지 못하면 1칸을 이동한다는 조건이 있었습니다. 그래서 1칸이 이동한지 먼저 체크한 후, 2칸이 이동가능하면 2칸을, 아니면 1칸으로 이동하는 로직을 만들어야 했습니다.
import java.io.*;
import java.util.*;
public class Main {
// 방향 벡터 (상, 하, 좌, 우)
static int[] dx = {1, -1, 0, 0}; // 세로, 행
static int[] dy = {0, 0, -1, 1}; // 가로, 열
public static void main(String[] args) throws IOException {
// Buffer로 받기
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 세로 크기 N
int m = Integer.parseInt(st.nextToken()); // 가로 크기 M
char[][] miro = new char[n][m];
for (int i = 0; i < n; i++) {
miro[i] = br.readLine().toCharArray(); // {'.', '.', '#', '#'}
}
// 큐로 이동
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{0, 0, 0}); // {x, y, time}
// 방문 확인
boolean[][] visited = new boolean[n][m];
visited[0][0] = true;
while (!queue.isEmpty()) {
int[] current = queue.poll(); // 현재 위치 불러오기
int current_x = current[0];
int current_y = current[1];
int time = current[2];
// 목적지 도착
if (current_x == n - 1 && current_y == m - 1) {
System.out.println(time);
return;
}
// 4방향 둘러보기
for (int dir = 0; dir < 4; dir++) {
int x = current_x + dx[dir]; // 행
int y = current_y + dy[dir]; // 열
// 한 칸 이동 (미로 안이고 길인 곳으로)
if (x >= 0 && y >= 0 && x < n && y < m && miro[x][y] == '.') {
int nx = x + dx[dir];
int ny = y + dy[dir];
// 두 칸 이동 시도
if (nx >= 0 && ny >= 0 && nx < n && ny < m && miro[nx][ny] == '.') {
if (!visited[nx][ny]) {
visited[nx][ny] = true;
queue.add(new int[]{nx, ny, time + 1});
}
// 두 칸 이동이 불가능 > 한 칸 이동
} else {
if (!visited[x][y]) {
visited[x][y] = true;
queue.add(new int[]{x, y, time + 1});
}
}
}
// // 한 칸 이동 (미로 안이고 길인 곳으로)
// if (x >= 0 && y >= 0 && x < n && y < m && miro[x][y] == '.' && !visited[x][y]) {
// int nx = x + dx[dir];
// int ny = y + dy[dir];
// // 두 칸 이동이 가능
// if (nx >= 0 && ny >= 0 && nx < n && ny < m && miro[nx][ny] == '.' && !visited[nx][ny]) {
// visited[nx][ny] = true;
// queue.add(new int[]{nx, ny, time + 1});
// // 두 칸 이동이 불가능 = 한 칸 이동
// } else {
// visited[x][y] = true;
// queue.add(new int[]{x, y, time + 1});
// }
// }
}
}
System.out.println(-1);
}
}
static int[] dx = {1, -1, 0, 0}; // 행(row) 이동
static int[] dy = {0, 0, -1, 1}; // 열(column) 이동
문제를 풀면서 방향벡터를 처음 알게 되었는데 이 dx,dy는 (1,0), (-1,0), (0,-1), (0,1)를 뜻하며 (0,0)을 기준으로 상하좌우의 위치를 나타냅니다. x,y에 방향벡터 즉, dx,dy좌표를 더함으로써 4방향으로 나아갈 수 있도록 도와줍니다.
그리고 BFS의 생명인 LinkedList로 Queue를 생성하고 여기에 x,y,time을 리스트로 넣은 후, 4방향을 탐색해가며 이동시키는 방식으로 진행하였습니다.
스터디원분들과 의논했던 점은 방문하지 않은 것을 굳이 체크해야하냐는 것이었지만 어차피 최단거리를 탐색하는 것이기 때문에 방문하지 않은 길을 탐색하는 것이 가장 효율적일 것이라는 결론이 나왔습니다.
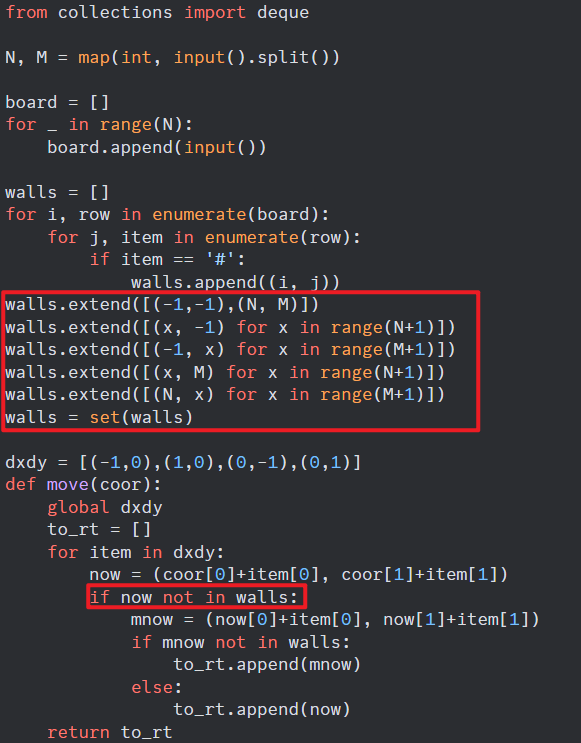
다른 스터디원분은 벽의 위치를 따로 추출해내서 이를 빼고 진행하는 방식의 코드도 있었는데 이 코드가 더욱 편리할 것이라는 의견도 나왔습니다. 이번 스터디에서도 다양한 코딩기법을 알 수 있었던 시간이었습니다.
'코딩 알고리즘 스터디' 카테고리의 다른 글
| 프로그래머스 Lv.1 신고 결과 받기 (1) | 2024.12.25 |
|---|---|
| 프로그래머스 Lv.2 메뉴 리뉴얼 (Java) (2) | 2024.12.16 |
| 프로그래머스 중급 블로그 (0) | 2024.12.04 |
| 코딩마스터스 (고급) 작곡 프로그램 (1) | 2024.12.03 |
| 코딩마스터스 (중급) 곰팡이 (1) | 2024.11.19 |