프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
- 문제 설명
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
- 제한 조건
n은 2이상 1000000이하의 자연수입니다.
입출력 예
| n | result |
| 10 | 4 |
| 5 | 3 |
- 입출력 예 설명
입출력 예 #1
1부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환
입출력 예 #2
1부터 5 사이의 소수는 [2,3,5] 3개가 존재하므로 3를 반환
- 코드 풀이 과정
처음 풀었을 땐, 반복문으로 모든 수에 소수 검사를 돌리려 했다.

그래서 검색해본 결과 소수를 판별하기 위해 나누어 볼때
제곱을 한 수 전까지만 나누어 계산하는 것이다.
class Solution {
public int solution(int n) {
int answer = 0;
for (int i = 2; i <= n; i++) {
int count = 0;
for (int j = 2; j <= Math.sqrt(i); j++) {
if (i % j == 0) {
count = 1;
break;
}
}
if (count == 0) answer++;
}
return answer;
}
}
그래도 느린 알고리즘이었기 때문에 이게 맞는 지 의심이 들었는데,
스터디를 하면서 에라토스테네스를 알게되었다.
에라토스테네스 체
- 배열을 모든 수가 소수라고 가정하고 초기화한다.
- 2부터 시작해서 특정 수의 배수에 해당하는 수를 모두 지운다. (지울 때 자기자신은 지우지 않고, 이미 지워진 수는 건너뛴다.)
- 배열에서 지워지지 않는 수를 모두 반환한다.
class Solution {
public int solution(int n) {
int answer = 0;
boolean[] isPrime = new boolean[n + 1];
for (int i = 2; i <= n; i++) {
isPrime[i] = true; // 모든 수를 소수로 가정
}
for (int i = 2; i * i <= n; i++) {
if (isPrime[i]) {
for (int j = i * i; j <= n; j += i) {
isPrime[j] = false;
}
}
}
for (int i = 2; i <= n; i++) {
if (isPrime[i]) answer++; // 소수가 true인 것만 카운트
}
return answer;
}
}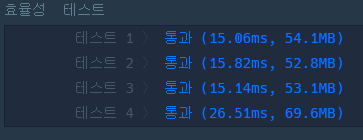
에라토스테네스를 발견하고 더욱 빠른 코드가 완성할 수 있었다!
'코딩 알고리즘 스터디' 카테고리의 다른 글
| 프로그래머스 Lv2. 타겟 넘버 (0) | 2024.10.14 |
|---|---|
| 프로그래머스 (고급) 친척 수 (0) | 2024.10.08 |
| 코딩마스터스 (중급) 밑장빼기 (1) | 2024.10.01 |
| 프로그래머스 Lv2. 뒤에 있는 큰 수 찾기 (0) | 2024.09.24 |
| 코딩 스터디 시작! (0) | 2024.09.09 |