보이는게 전부가 아님을 꼭 명심하세요!

기준 = 유의수준 : 직선
상관계수( r ) : 누가 강한 관계를 가졌는지 수치화 한것.
- 강한, 약한 관계에 대한 가이드라인을 제시한다.
- ~1 또는 1에 가까울 수록 강한 관계를 가졌다.
- 기준 : 1 ~ 0.5(강한), ~ 0.2(중간), ~ 0.1(약한), ~ 0(관계없음)
- 절대값 r로하면 상관관계를 살펴보는 값이다.
p-value : 0.05(5%)를 기준으로 차이를 판결하는 것이다.
p-value가 0.05보다 작을 수록 차이가 큰것, 0.05보다 크면 차이가 작은것
0에 수렵하면 관련이 많다라는 뜻이다.
1. 산점도 (Scatter)
그대로 점을 찍어서 그래프를 그려 봅시다.
직선(Linarity)를 보는 관점이 중요합니다.

산점도 코드
- plt.scatter(air['숫자'],air[ '숫자'])
plt.scatter('숫자', '숫자', data=air)
- sns.scatterplot(x='숫자', y='숫자', data=air)

- jointplot(x='숫자', y='숫자', data=air)

- regplot(x='숫자', y='숫자', data=air, line_kws={'color': 'darkred'})

- sns.pairplot(air)
단점 : 시간이 많이 걸림..

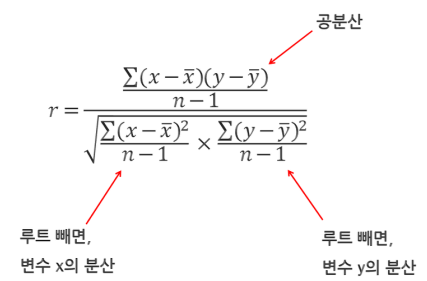
2. 공분산(covariance), 상관계수(correlation efficient)
각점들이 얼마나 직선으로 모여 있는지 계산합니다.
- 상관관계 두가지 : 공분산, 상관계수
상관계수 : r이 -1 또는 1에 가까울 수록 강한 상관관계를 나타냅니다.
v-value : 0.05를 기준으로 작을 수록 상관, 차이가 있다고 검정할 수 있습니다.
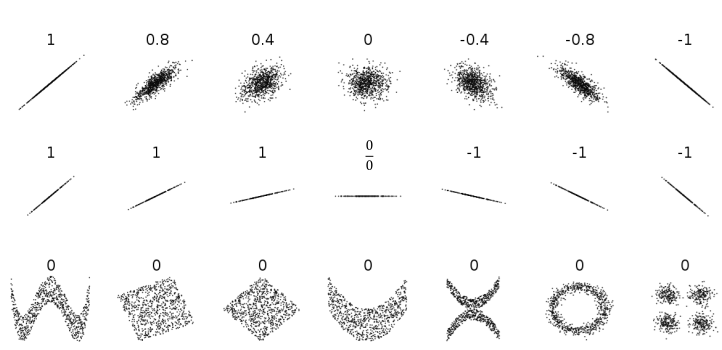
상관계수의 한계
하지만 선형 관계만 수치화해주기 때문에
비선형 관계, 직선의 기울기은 고려하지 않는다.
상관분석 코드
상관분석 : 그래프로만은 판단이 어려우니, 상관계수가 유의미한지 검정
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as spst
- spst.pearsonr('숫자','숫자')
import scipy.stats as spst
# 상관계수와 p-value
result = spst.pearsonr(air['Temp'], air['Ozone'])
print(f'r : {result[0]}')
print(f'pv : {result[1]}')
※ 주의
notnull, notna()로 NaN값을 없애서 데이터의 크기가 다르면 안된다.
상관분석은 데이터의 크기가 같아야 한다.
temp = air.loc[air['Solar.R'].notnull()]
# result = spst.pearsonr(temp['Solar.R'], air['Ozone'])
result = spst.pearsonr(temp['Solar.R'], temp['Ozone'])
- 데이터프레임.corr()
air.corr()
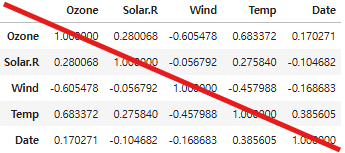
- heatmap으로 시각화
plt.figure(figsize = (8, 8))
sns.heatmap(air.corr(),
annot = True, # 숫자(상관계수) 표기 여부
fmt = '.3f', # 숫자 포멧 : 소수점 3자리까지 표기
cmap = 'RdYlBu_r', # 칼라맵
vmin = -1, vmax = 1) # 값의 최소, 최대값
plt.show()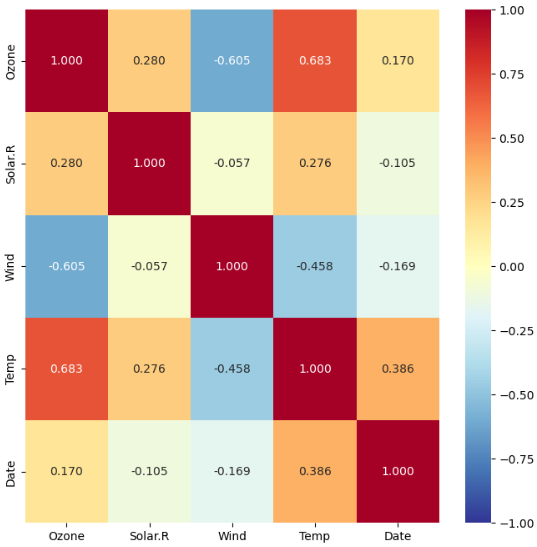
'KT AIVLE School > 데이터 분석 및 의미 찾기' 카테고리의 다른 글
| 이변량 분석 : 숫자 → 범주 (0) | 2024.09.13 |
|---|---|
| 이변량 분석 : 범주 → 범주 (0) | 2024.09.13 |
| 이변량 분석 : 범주 → 숫자 (0) | 2024.09.12 |
| 평균 추정과 신뢰구간 (0) | 2024.09.12 |
| 가설검정 (0) | 2024.09.11 |
